Home >> My Performance >> My Topic Test Performance >> My Question Performance
My Question Performance Summary in Full Tests !
Questions Available: 13
Questions Attempted: 10
Number of Attempts: 15
Correct Attempts: 8
Total Time Spent: 00:30
Avg Time Per Question: 00:02
My Question Performance Summary in Full Tests
When an \(\alpha\)-particle of mass m moving with velocity v bombards on a heavy nucleus of charge Ze, its distance of closest approach from the nucleus depends on m as
(1). \(\displaystyle \frac{1}{\sqrt{m}}\)
(2). \(\displaystyle \frac{1}{m^2}\)
(3). \(\displaystyle m\)
(4). \(\displaystyle \frac{1}{m}\)
(1). \(\displaystyle \frac{1}{\sqrt{m}}\)
(2). \(\displaystyle \frac{1}{m^2}\)
(3). \(\displaystyle m\)
(4). \(\displaystyle \frac{1}{m}\)
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
A particle of mass m is moving around the origin with a constant force F pulling it towards the origin. If Bohr model is used to describe its motion, the radius of the \(\text{n}^{\text{th}}\) orbit and the particle's speed v in the orbit depends on n as
(1). \(\text{r}\propto{n^{\frac{4}{3}}}\), \(\text{v}\propto{n^{-\frac{1}{3}}}\)
(2). \(\text{r}\propto{n^{\frac{1}{3}}}\), \(\text{v}\propto{n^{\frac{1}{3}}}\)
(3). \(\text{r}\propto{n^{\frac{1}{3}}}\), \(\text{v}\propto{n^{\frac{2}{3}}}\)
(4). \(\text{r}\propto{n^{\frac{2}{3}}}\), \(\text{v}\propto{n^{\frac{1}{3}}}\)
(1). \(\text{r}\propto{n^{\frac{4}{3}}}\), \(\text{v}\propto{n^{-\frac{1}{3}}}\)
(2). \(\text{r}\propto{n^{\frac{1}{3}}}\), \(\text{v}\propto{n^{\frac{1}{3}}}\)
(3). \(\text{r}\propto{n^{\frac{1}{3}}}\), \(\text{v}\propto{n^{\frac{2}{3}}}\)
(4). \(\text{r}\propto{n^{\frac{2}{3}}}\), \(\text{v}\propto{n^{\frac{1}{3}}}\)
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
De-Broglie wavelength of an electron orbiting in the n = 2 state of hydrogen atom is close to (Given Bohr radius = 0.052 nm)
(1). 2.67 nm
(2). 0.067 nm
(3). 0.67 nm
(4). 1.67 nm
(1). 2.67 nm
(2). 0.067 nm
(3). 0.67 nm
(4). 1.67 nm
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
Given below are two statements :
Statement I : Atoms are electrically neutral as they contain equal number of positive and negative charges .
Statement II : Atoms of each element are stable and emit their characteristic spectrum .
In the light of the above statements, choose the most appropriate answer from the options given below :
(1). Statement I is correct but Statement II is incorrect .
(2). Statement I is incorrect but Statement II is correct .
(3). Both Statement I and Statement . II are correct .
(4). Both Statement I and Statement II are incorrect .
Statement I : Atoms are electrically neutral as they contain equal number of positive and negative charges .
Statement II : Atoms of each element are stable and emit their characteristic spectrum .
In the light of the above statements, choose the most appropriate answer from the options given below :
(1). Statement I is correct but Statement II is incorrect .
(2). Statement I is incorrect but Statement II is correct .
(3). Both Statement I and Statement . II are correct .
(4). Both Statement I and Statement II are incorrect .
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
Match List I with List II
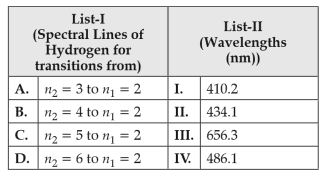
Choose the correct answer from the options given below
(1). A - IV , B - III , C - I , D - II
(2). A - I , B - II , C - III , D - IV
(3). A - II , B - I , C - IV , D - III
(4). A - III , B - IV , C - II , D - I

Choose the correct answer from the options given below
(1). A - IV , B - III , C - I , D - II
(2). A - I , B - II , C - III , D - IV
(3). A - II , B - I , C - IV , D - III
(4). A - III , B - IV , C - II , D - I
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
In hydrogen spectrum, the shortest wavelength in the Balmer series is \(\lambda\). The shortest wavelength in the Bracket series is
(1). \(4\, \lambda\)
(2). \(9\, \lambda\)
(3). \(16\, \lambda\)
(4). \(2\, \lambda\)
(1). \(4\, \lambda\)
(2). \(9\, \lambda\)
(3). \(16\, \lambda\)
(4). \(2\, \lambda\)
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
The radius of inner most orbit of hydrogen atom is \(\displaystyle 5.3 \times 10^{-11} \) m. What is the radius of third allowed orbit of hydrogen atom?
(1). \(\displaystyle 1.06\, \mathring{A} \)
(2). \(\displaystyle 1.59\, \mathring{A} \)
(3). \(\displaystyle 4.77\, \mathring{A} \)
(4). \(\displaystyle 0.53\, \mathring{A} \)
(1). \(\displaystyle 1.06\, \mathring{A} \)
(2). \(\displaystyle 1.59\, \mathring{A} \)
(3). \(\displaystyle 4.77\, \mathring{A} \)
(4). \(\displaystyle 0.53\, \mathring{A} \)
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
Let T1 and T2 be the energy of an electron in the first and second excited states of hydrogen atom, respectively. According to the Bohr’s model of an atom, the ratio T1 : T2 is :
(1). 1:04
(2). 4:01
(3). 4:09
(4). 9 : 4
(1). 1:04
(2). 4:01
(3). 4:09
(4). 9 : 4
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
For which one of the following, Bohr model is not valid?
(1). Singly ionised helium atom (\(He^+\) )
(2). Deuteron atom
(3). Singly ionised neon atom (\(Ne^+\) )
(4). Hydrogen atom
(1). Singly ionised helium atom (\(He^+\) )
(2). Deuteron atom
(3). Singly ionised neon atom (\(Ne^+\) )
(4). Hydrogen atom
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
The total energy of an electron in an atom in an orbit is −3 4 . eV. Its kinetic and potential energies are, respectively:
(1). −3.4 eV, −6.8 eV
(2). 3.4 eV, −6.8 eV
(3). 3.4 eV, 3.4 eV
(4). −3.4 eV, −3.4 eV
(1). −3.4 eV, −6.8 eV
(2). 3.4 eV, −6.8 eV
(3). 3.4 eV, 3.4 eV
(4). −3.4 eV, −3.4 eV
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
The ratio of kinetic energy to the total energy of an electron in a Bohr orbit of the hydrogen atom, is
(1). 2 : − 1
(2). 1 : − 1
(3). 1:01
(4). 1 : −2
(1). 2 : − 1
(2). 1 : − 1
(3). 1:01
(4). 1 : −2
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
The ratio of wavelengths of the last line of Balmer series and the last line of Lyman series is
(1). 2
(2). 1
(3). 4
(4). 0.5
(1). 2
(2). 1
(3). 4
(4). 0.5
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
Given the value of Rydberg constant is \(10\,\text{m}^{-1}\), the wave number of the last line of the Balmer series in hydrogen spectrum will be
(1). \(0.5 \times 10^7\,\text{m}^{-1}\)
(2). \(0.25 \times 10^7\,\text{m}^{-1}\)
(3). \(2.5 \times 10^7\,\text{m}^{-1}\)
(4). \(0.025 \times 10^4\,\text{m}^{-1}\)
(1). \(0.5 \times 10^7\,\text{m}^{-1}\)
(2). \(0.25 \times 10^7\,\text{m}^{-1}\)
(3). \(2.5 \times 10^7\,\text{m}^{-1}\)
(4). \(0.025 \times 10^4\,\text{m}^{-1}\)
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
