Home >> My Performance >> My Topic Test Performance >> My Question Performance
My Question Performance Summary in Full Tests !
Questions Available: 18
Questions Attempted: 10
Number of Attempts: 15
Correct Attempts: 8
Total Time Spent: 00:30
Avg Time Per Question: 00:02
My Question Performance Summary in Full Tests
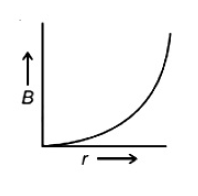
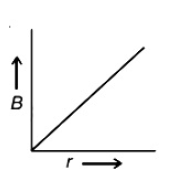
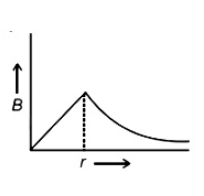
A thick current carrying cable of radius 'R' carries current 'I' uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance 'r' from the axis of the cable is represented by
(1).
(2).
(3).
(4).
(1).

(2).

(3).

(4).

Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
A long solenoid of 50 cm length having 100 turns carries a current of 2.5 A. The magnetic field at the centre of the solenoid is: (\(\mu_0\, =\, 4\, \pi \times 10^{−7}\,T\, m\,A^{−1}\))
(1). \(3.14 \times 10^{−4}\,T\)
(2). \(6.28 \times 10^{−5}\,T\)
(3). \(3.14 \times 10^{−5}\,T\)
(4). \(6.28 \times 10^{−4}\,T\)
(1). \(3.14 \times 10^{−4}\,T\)
(2). \(6.28 \times 10^{−5}\,T\)
(3). \(3.14 \times 10^{−5}\,T\)
(4). \(6.28 \times 10^{−4}\,T\)
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
A model for quantized motion of an electron in a uniform magnetic field B states that the flux passing through the orbit of the electron is n(h/e) where n is an integer, h is Planck's constant and e is the magnitude of electron's charge. According to the model, the magnetic moment of an electron in its lowest energy state will be (m is the mass of the electron)
(1). \(\displaystyle \frac{\text{heB}}{2\pi\text{m}}\)
(2). \(\displaystyle \frac{\text{he}}{\pi\text{m}}\)
(3). \(\displaystyle \frac{\text{he}}{2\pi\text{m}}\)
(4). \(\displaystyle \frac{\text{heB}}{\pi\text{m}}\)
(1). \(\displaystyle \frac{\text{heB}}{2\pi\text{m}}\)
(2). \(\displaystyle \frac{\text{he}}{\pi\text{m}}\)
(3). \(\displaystyle \frac{\text{he}}{2\pi\text{m}}\)
(4). \(\displaystyle \frac{\text{heB}}{\pi\text{m}}\)
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
A tightly wound 100 turns coil of radius 10 cm carries a current of 7A. The magnitude of the magnetic field at the centre of the coil is (Take permeability of free space as 4π × 10−7 SI units):
(1). 44 mT
(2). 4.4 T
(3). 4.4 mT
(4). 44 T
(1). 44 mT
(2). 4.4 T
(3). 4.4 mT
(4). 44 T
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
If the galvanometer G does not show any deflection in the circuit shown, the value of R is given by
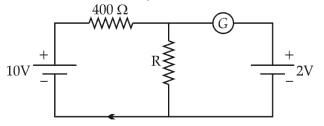
(1). 50 Ω
(2). 100 Ω
(3). 400 Ω
(4). 200 Ω

(1). 50 Ω
(2). 100 Ω
(3). 400 Ω
(4). 200 Ω
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
A very long conducting wire is bent in a semi-circular shape from A to B as shown in figure. The magnetic field at point P for steady current configuration is given by
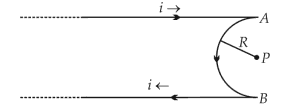
(1). \(\displaystyle\frac{µ_0i}{4R}\) pointed away from the page
(2). \(\displaystyle\frac{µ_0i}{4R}\) \(\displaystyle[1 - \frac{2}{\pi}]\) pointed away from the page
(3). \(\displaystyle\frac{µ_0i}{4R}\) \(\displaystyle[1 - \frac{2}{\pi}]\) pointed the page
(4). \(\displaystyle\frac{µ_0i}{4R}\) pointed into the page

(1). \(\displaystyle\frac{µ_0i}{4R}\) pointed away from the page
(2). \(\displaystyle\frac{µ_0i}{4R}\) \(\displaystyle[1 - \frac{2}{\pi}]\) pointed away from the page
(3). \(\displaystyle\frac{µ_0i}{4R}\) \(\displaystyle[1 - \frac{2}{\pi}]\) pointed the page
(4). \(\displaystyle\frac{µ_0i}{4R}\) pointed into the page
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
A wire carrying a current I along the positive x-axis has length L. It is kept in a magnetic field \(\vec{B}\) = \(\left( 2\hat{i} + 3\hat{j} - 4\hat{j}\right)\)T. The magnitude of the magnetic force acting on the wire is
(1). \(\sqrt{5}/L\)
(2). \(5/L\)
(3). \(\sqrt{3}/L\)
(4). \(3/IL\)
(1). \(\sqrt{5}/L\)
(2). \(5/L\)
(3). \(\sqrt{3}/L\)
(4). \(3/IL\)
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
From Ampere's circuital law for a long straight wire of circular cross section carrying a steady current, the variation of magnetic field in the inside and outside region of the wire is:
(1). Uniform and remains constant for both the regions.
(2). A linearly increasing function of distance upto the boundary of the wire and then linearly decreasing for the outside region.
(3). A linearly increasing function of distance r upto the boundary of the wire and then decreasing one with \(\displaystyle \frac{1}{r}\) dependence for the outside region.
(4). A linearly decreasing function of distance upto the boundary of the wire and then a linearly increasing one for the outside region.
(1). Uniform and remains constant for both the regions.
(2). A linearly increasing function of distance upto the boundary of the wire and then linearly decreasing for the outside region.
(3). A linearly increasing function of distance r upto the boundary of the wire and then decreasing one with \(\displaystyle \frac{1}{r}\) dependence for the outside region.
(4). A linearly decreasing function of distance upto the boundary of the wire and then a linearly increasing one for the outside region.
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
Given below are two statements.
Statement I : Biot-Savart's law gives us the expression for the magnetic field strength of an infinitesimal current element (Idl) of a current carrying conductor only.
Statement II : Biot-Savart's law is analogous to Coulomb's inverse square law of charge q, with the former being related to the field produced by a scalar source, Id while the later being produced by a vector source, q. In light of above statements choose the most appropriate answer from the options given below
(1). Both Statement I and Statement II are correct
(2). Both Statement I and Statement II are incorrect
(3). Statement I is correct and Statement II is incorrect
(4). Statement I is incorrect and Statement II is correct
Statement I : Biot-Savart's law gives us the expression for the magnetic field strength of an infinitesimal current element (Idl) of a current carrying conductor only.
Statement II : Biot-Savart's law is analogous to Coulomb's inverse square law of charge q, with the former being related to the field produced by a scalar source, Id while the later being produced by a vector source, q. In light of above statements choose the most appropriate answer from the options given below
(1). Both Statement I and Statement II are correct
(2). Both Statement I and Statement II are incorrect
(3). Statement I is correct and Statement II is incorrect
(4). Statement I is incorrect and Statement II is correct
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
An infinitely long straight conductor carries a current of 5A as shown. An electron is moving with a speed of 105 m ∕ s parallel to the conductor. The perpendicular distance between the electron and the conductor is 20 cm at an instant. Calculate the magnitude of the force experienced by the electron at that instant.
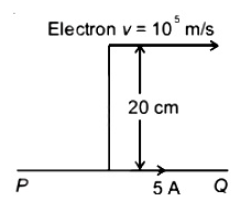
(1). 4 × 10−20 N
(2). 8π × 10−20 N
(3). 4π × 10−20 N
(4). 8 × 10−20 N

(1). 4 × 10−20 N
(2). 8π × 10−20 N
(3). 4π × 10−20 N
(4). 8 × 10−20 N
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
In the product \(\vec{F} = q \left(\vec{v} × \vec{B}\right) = q\vec{v} × \left( B\hat{i} + B\hat{j} + B_0\hat{k}\right)\) For q = 1 and \(\vec{v} = 2\hat{i} + 4\hat{j} + 6\hat{k}\) and \(\vec{F} = 4\hat{i} - 20\hat{j} + 12\hat{k}\) What will be the complete expression for \(\vec{B}\)
(1). \(-8\hat{i} - 8\hat{j} - 6\hat{k}\)
(2). \(-6\hat{i} - 6\hat{j} - 8\hat{k}\)
(3). \(8\hat{i} + 8\hat{j} - 6\hat{k}\)
(4). \(6\hat{i} + 6\hat{j} - 8\hat{k}\)
(1). \(-8\hat{i} - 8\hat{j} - 6\hat{k}\)
(2). \(-6\hat{i} - 6\hat{j} - 8\hat{k}\)
(3). \(8\hat{i} + 8\hat{j} - 6\hat{k}\)
(4). \(6\hat{i} + 6\hat{j} - 8\hat{k}\)
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
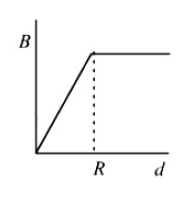
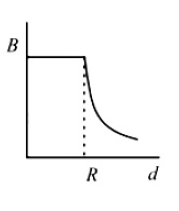
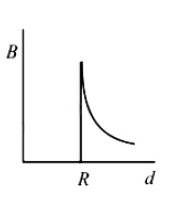
A cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the centre of the conductor, is correctly represented by the figure
(1).
(2).
(3).
(4).
(1).

(2).

(3).

(4).

Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
Ionized hydrogen atoms and α-particles with same momenta enters perpendicular to a constant magnetic field, B. The ratio of their radii of their paths rH : rα wil be
(1). 1 : 4
(2). 2 : 1
(3). 1 : 2
(4). 4 : 1
(1). 1 : 4
(2). 2 : 1
(3). 1 : 2
(4). 4 : 1
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
A metallic rod of mass per unit length 0.5 kgm−1 is lying horizontally on a smooth inclined plane which makes an angle of \(30^\circ\) with the horizontal. The rod is not allowed to slide down by flowing a current through it when a magnetic field of induction 0.25 T is acting on it in the vertical direction. The current flowing in the rod to keep it stationary is
(1). 7.14 A
(2). 5.98 A
(3). 14.76 A
(4). 11.32 A
(1). 7.14 A
(2). 5.98 A
(3). 14.76 A
(4). 11.32 A
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
Current sensitivity of a moving coil galvanometer is 5 div/mA and its voltage sensitivity (angular deflection per unit voltage applied) is 20 div/V. The resistance of the galvanometer is
(1). 40 Ω
(2). 25 Ω
(3). 250 Ω
(4). 500 Ω
(1). 40 Ω
(2). 25 Ω
(3). 250 Ω
(4). 500 Ω
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
An arrangement of three parallel straight wires placed perpendicular to plane of paper carrying same current I along the same direction as shown in figure. Magnitude of force per unit length on the middle wire ‘B’ is given by
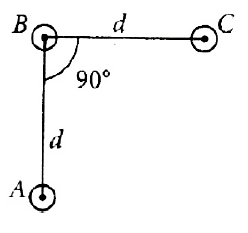
(1). \(\displaystyle\frac{2µ_0I^2}{πd}\)
(2). \(\displaystyle\frac{2µ_0I^2}{πd}\)
(3). \(\displaystyle\frac{µ_0I^2}{\sqrt{2}πd}\)
(4). \(\displaystyle\frac{µ_0I^2}{2πd}\)

(1). \(\displaystyle\frac{2µ_0I^2}{πd}\)
(2). \(\displaystyle\frac{2µ_0I^2}{πd}\)
(3). \(\displaystyle\frac{µ_0I^2}{\sqrt{2}πd}\)
(4). \(\displaystyle\frac{µ_0I^2}{2πd}\)
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
A long straight wire of radius a carries a steady current I. The current is uniformly distributed over its cross-section. The ratio of the magnetic fields B and B', at radial distances \(\displaystyle\frac{a}{2}\) and \(2a\) respectively, from the axis of the wire is
(1). \(1\)
(2). \(4\)
(3). \(\displaystyle\frac{1}{4}\)
(4). \(\displaystyle\frac{1}{2}\)
(1). \(1\)
(2). \(4\)
(3). \(\displaystyle\frac{1}{4}\)
(4). \(\displaystyle\frac{1}{2}\)
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
A square loop ABCD carrying a current is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be
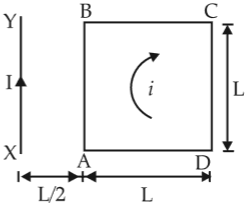
(1). \(\displaystyle\frac{2µ_0I iL}{3π}\)
(2). \(\displaystyle\frac{µ_0I iL}{2π}\)
(3). \(\displaystyle\frac{2µ_0I i}{3π}\)
(4). \(\displaystyle\frac{µ_0I i}{2π}\)

(1). \(\displaystyle\frac{2µ_0I iL}{3π}\)
(2). \(\displaystyle\frac{µ_0I iL}{2π}\)
(3). \(\displaystyle\frac{2µ_0I i}{3π}\)
(4). \(\displaystyle\frac{µ_0I i}{2π}\)
Number of Attempts: 2
Correct Attempts: 1
Time Taken: 00:04
Average Time: 00:02
