The displacement of a particle executing simple harmonic motion is given by \(y = A_0 + A sin ω t + B cos ω t\). Then the amplitude of its oscillation is given by

(1). \(A + B\)
(2). \( A_0 + \sqrt{A^2 + B^2}\)
(3). \(\sqrt{A^2 + B^2}\)
(4). \(\sqrt{{A_0}^2 + \left(A + B\right)^2}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

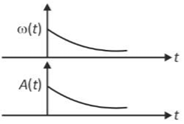
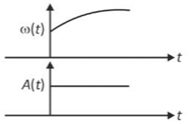
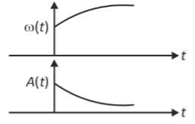
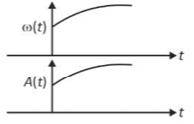
In an oscillating spring mass system, a spring is connected to a box filled with sand. As the box oscillates, sand leaks slowly out of the box vertically so that the average frequency \(\omega\left(\text{t}\right)\) and average amplitude \(\text{A}\left(\text{t}\right)\) of the system change with time t. Which one of the following options schematically depicts these changes correctly?

(1).
(2).
(3).
(4).

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

Two identical point masses P and Q, suspended from two separate massless springs of spring constants \(\text{k}_1\) and \(\text{k}_2\), respectively, oscillate vertically. if their maximum speeds are the same, the ratio (\( \text{A}_Q\)/\(\text{A}_P\)) of the amplitude \(\text{A}_Q\) of mass Q to the amplitude \(\text{A}_P\) of mass P is

(1). \(\displaystyle \sqrt{\frac{\text{K}_1}{\text{K}_2}}\)
(2). \(\displaystyle \frac{\text{K}_2}{\text{K}_1}\)
(3). \(\displaystyle \frac{\text{K}_1}{\text{K}_2}\)
(4). \(\displaystyle \sqrt{\frac{\text{K}_2}{\text{K}_1}}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

If \(x = 5sin (πt + π/3) m\) represents the motion of a particle executing simple harmonic motion, the amplitude and time period of motion,respectively, are

(1). \(5cm,\, 2s\)
(2). \(5m, \, 2s\)
(3). \(5cm, \, 1s\)
(4). \(5m,\, 1s\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

If the mass of the bob in a simple pendulum is increased to thrice its original mass and its length is made half its original length, then the new time period of oscillation is \(x/2\) times its original time period. Then the value of x is:

(1). \(\sqrt{3}\)
(2). \(\sqrt{2}\)
(3). \(2 \sqrt{3}\)
(4). \(4\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

The x-t graph of a particle performing simple harmonic motion is shown in the figure. The acceleration of the particle at \(t = 2s\) is


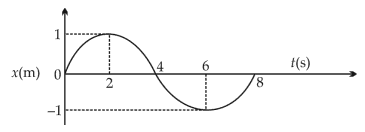
(1). \(\displaystyle \frac{-π^2}{8} ms^{-2}\)
(2). \(\displaystyle \frac{π^2}{16}ms^{-2}\)
(3). \(\displaystyle \frac{-π^2}{16} ms^{-2}\)
(4). \(\displaystyle \frac{π^2}{8} ms^{-2}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

Two pendulums of length \(121\, cm\) and \(100\, cm\) start vibrating in phase. At some instant, the two are at their mean position in the same phase. The minimum number of vibrations of the shorter pendulum after which the two are again in phase at the mean position is:

(1). \(11\)
(2). \(9\)
(3). \(10\)
(4). \(8\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A body is executing simple harmonic motion with frequency\(\, 'n'\), the frequency of its potential energy is

(1). \(n\)
(2). \(2n\)
(3). \(3n\)
(4). \(4n\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A spring is stretched by 5 cm by a force 10 N. The time period of the oscillations when a mass of 2 Kg is suspended by it is

(1). 0.628 S
(2). 0.0628 S
(3). 6.28 S
(4). 3.14 S

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

The phase difference between displacement and acceleration of a particle in a simple harmonic motion is:

(1). \(\displaystyle \frac{3\,\pi}{2}\) rad
(2). \(\displaystyle \frac{\pi}{2}\) rad
(3). \(zero\)
(4). \(\pi \) rad

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

Average velocity of a particle executing SHM in one complete vibration is

(1). \(\displaystyle \text{zero}\)
(2). \(\displaystyle \frac{Aω}{2}\)
(3). \(\displaystyle Aω\)
(4). \(\displaystyle \frac{Aω^2}{2}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

The radius of circle, the period of revolution, initial position and sense of revolution are indicated in the figure.

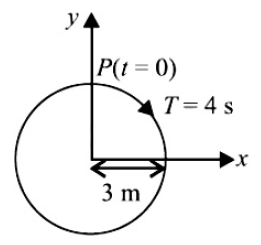
y - projection of the radius vector of rotating particle \(P\) is

(1). \(y(t) = 3 cos \left(\frac{πt}{2}\right)\), where y in m
(2). \(y(t) = −3 cos 2 π t\), where y in m
(3). \(y(t) = 4 sin \left(\frac{πt}{2}\right)\), where y in m
(4). \(y(t) = 3 cos \left(\frac{3πt}{2}\right) \), where y in m

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A pendulum is hung from the roof of a sufficiently high building and is moving freely to and fro like a simple harmonic oscillator. The acceleration of the bob of the pendulum is \(20ms^{−2}\) at a distance of 5m from the mean position. The time period of oscillation is

(1). \(2πs\)
(2). \(πs\)
(3). \(2s\)
(4). \(1s\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A spring of force constant k is cut into lengths of ratio \(1 : 2 : 3\). They are connected in series and the new force constant is \(k'\).Then they are connected in parallel and force constant is \(k''\).Then \(k' : k''\) is

(1). \(1 : 9\)
(2). \(1 : 11\)
(3). \(1 : 14\)
(4). \(1 : 6\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A particle executes linear simple harmonic motion with an amplitude of \(3\, \text{cm}\). When the particle is at \(2\, \text{cm}\) from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is

(1). \(\displaystyle \frac{\sqrt{5}}{2π}\)
(2). \(\displaystyle \frac{4π}{\sqrt{5}}\)
(3). \(\displaystyle \frac{2π}{\sqrt{3}}\)
(4). \(\displaystyle \frac{\sqrt{5}}{π}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02