The average thermal energy for a monoatomic gas is (where,\(k_ B\) is Boltzmann constant and T is absolute temperature.)

(1). \(\displaystyle \frac{3}{2}k_B\,T\)
(2). \(\displaystyle \frac{5}{2}k_B\,T\)
(3). \(\displaystyle \frac{7}{2}k_B\,T\)
(4). \(\displaystyle \frac{1}{2}k_B\,T\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

The following graph represents the T - V curves of an ideal gas ( where T is the temperature and V the volume ) at three pressures P1 , P2 and P3 compared with those of Charles's law represented as dotted lines .


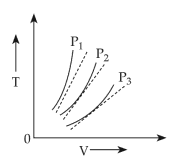
(1). P₂ > P₁ > P₃
(2). P₁ > P₂ > P₃
(3). P₃ > P₂ > P₁
(4). P₁ > P₃ > P₂

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

Match Column l with Column ll andchoose the correct match fromthegiven choices.


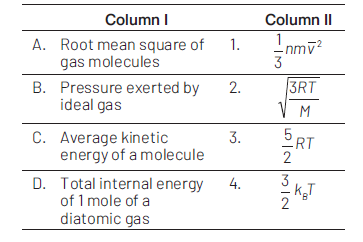
(1). A-3, B-1, C-4, D-2
(2). A-2, B-3, C-4, D-1
(3). A-2, B-1, C-4, D-3
(4). A-3, B-2, C-1, D-4

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

The mean free path l for a gas,with molecular diameter d and number density n can be expressed as

(1). \(\displaystyle \frac{1}{\sqrt{2}n\pi d^2}\)
(2). \(\displaystyle \frac{1}{\sqrt{2}n^2\pi d^2}\)
(3). \(\displaystyle \frac{1}{\sqrt{2}n^2\pi^2 d^2}\)
(4). \(\displaystyle \frac{1}{\sqrt{2}n\pi d}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A cylinder contains hydrogen gas at pressure of 249 kPa and temperature 27°C. Its density is (\(R = 8.3\, J mol^{ −1} K^{−1}\) )

(1). \(0.2\, kg/m^3\)
(2). \( 0.1\, kg/m^3\)
(3). \( 0.02 \, kg/m^3\)
(4). \(0.5 \, kg/m^3\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

Increase in temperature of a gas filled in a container would lead to

(1). increase in its kinetic energy
(2). decrease in its pressure
(3). decrease in intermolecular distance
(4). increase in its mass

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

At what temperature will the rms speed of oxygen molecules become just sufficient for escaping from the Earth’s atmosphere?
(Given: mass of oxygen molecule,\(m = 2.76 × 10^−{26}\, kg\) ,Boltzmann’s constant\(k_B = 1.38 10^{-23} J K^{ −1}\))

(1). \(5.016 \times 10^4\, K\)
(2). \(8.326 \times 10^4\, K\)
(3). \(2.508 \times 10^4\, K\)
(4). \(1.254 \times 10^4\, K\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A gas mixture consists of 2 moles of \(O_2\) and 4 moles of \(A_r\) at temperature T. Neglecting all vibrational modes, the total internal energy of the system is

(1). 4 RT
(2). 15 RT
(3). 9 RT
(4). 11 RT

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

The molecules of a given mass of a gas have r.m.s. velocity of \(200\, \text{ms}^{−1}\) at \(27^\circ \text{C}\) and \(1.0 \times 10^5 \text{Nm}^{−2}\) pressure. When the temperature and pressure of the gas are respectively, \(127^ \circ \text{C}\) and \(0.05 \times 10^5 \text{Nm}^{ −2}\) , the rms velocity of its molecules in \(\text{ms}^{ −1}\) is

(1). \(\displaystyle \frac{400}{\sqrt{3}}\)
(2). \(\displaystyle \frac{100\sqrt{2}}{3}\)
(3). \(\displaystyle \frac{100}{3}\)
(4). \(\displaystyle100\sqrt{2}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02