The maximum elongation of a steel wire of 1m length if the elastic limit of steel and its Young's modulus, respectively, are 8 × 10⁸ Nm⁻² and 2 ×10¹¹ Nm⁻², is:

(1). 4 mm
(2). 0.4 mm
(3). 40 mm
(4). 8 mm

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A metallic bar of Young's modulus, \(0.5 × 10^{11}Nm^{−2}\) and coefficient of linear thermal expansion \(10^{−5^\circ}C^{−1}\), length 1m and area of cross section \(10^{−3}m^2\) is heated from \(0^\circ C\) to \(100^\circ C\) with out expansion or bending. The compressive force developed in it is:

(1). 5 × 10³ N
(2). 50 × 10³ N
(3). 100 × 10³ N
(4). 2 × 10³ N

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

Let a wire be suspended from the ceiling (rigid support) and stretched by a weight W attached at its free end. The longitudinal stress at anypoint of cross-sectional area A of the wire is

(1). \(\displaystyle \frac{W}{A}\)
(2). \(\displaystyle \frac{W}{2A}\)
(3). \(Zero\)
(4). \(\displaystyle\frac{2W}{A}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

Three identical heat conducting rods are connected in series as shown in the figure. The rods on the sides have thermal conductivity 2K while that in the middle has thermal conductivity K. The left end of the combination is maintained at temperature 3T and the right end at T. The rods are thermally insulated from outside. In steady state, temperature at the left junction is \(\text{T}_1\), and that at the right junction is \(\text{T}_2\). The ratio \(\text{T}_1\,\\,\text{T}_2\) is


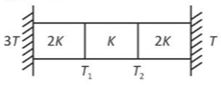
(1). \(\displaystyle \frac{5}{4}\)
(2). \(\displaystyle \frac{3}{2}\)
(3). \(\displaystyle \frac{4}{3}\)
(4). \(\displaystyle \frac{5}{3}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A thin flat circular disc of radius 4.5 cm is placed gently over the surface of water. If surface tension of water is 0.07Nm⁻¹, then the excess force required to take it away from the surface is

(1). 19.8 mN
(2). 198 N
(3). 1.98 mN
(4). 99 N

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

The amount of energy required to form a soap bubble of radius 2 cm from a soap solution is nearly (surface tension of soap solution = 0.03 Nm⁻¹)

(1). \(5.06 × 10^{−4}J\)
(2). \(3.01 × 10^{−4}J\)
(3). \(50.1 × 10^{−4}J\)
(4). \(30.16 × 10^{−4}J\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

The venturi-meter works on

(1). Bernoulli's principle
(2). The principle of parallel axes
(3). The principle of perpendicular axes
(4). Huygens's principle

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A spherical ball is dropped in a long column of a highly viscous liquid.The curve in the graph shown, which represents the speed of the ball (v) as a function of time (t) is


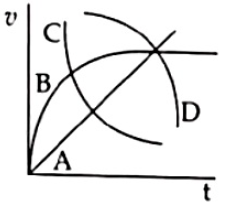
(1). A
(2). B
(3). C
(4). D

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

If a soap bubble expands, the pressure inside the bubble

(1). Decreases
(2). Increases
(3). Remains the same
(4). Is equal to the atmospheric pressure

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

Given below are two statements : One is labelled as Assertion (A) and the other is labelled as Reason (R).
Assertion (A): The stretching of a spring is determined by the shear modulus of the material of the spring.
Reason (R): A coil spring of copper has more tensile strength than a steel spring of same dimensions.
In the light of the above statements, choose the most appropriate answer from the options given below

(1). Both (A) and (R) are true and (R) is the correct explanation of (A)
(2). Both (A) and (R) are true and (R) is not the correct explanation of (A)
(3). (A) is true but (R) is false
(4). (A) is false but R ) is true

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A capillary tube of radius r is immersed in water and water rises in it to a height h. The mass of the water in the capillary is 5g. Another capillary tube of radius 2r is immersed in water. The mass of water that will rise in this tube is :

(1). 5.0 g
(2). 10.0 g
(3). 20.0 g
(4). 2.5 g

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A copper rod of 88 cm and an aluminium rod of unknown length have their increase in length independent of increase in temperature. The length of aluminium rod is \(\left(\alpha_{Cu} = 1.7 × 10^{−5}K^{−1}, \alpha_{Al} = 2.2 × 10^{−5}K^{−1}\right)\)

(1). 68 cm
(2). 6.8 cm
(3). 113.9 cm
(4). 88 cm

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A small hole of area of cross-section \(2 mm^2\) is present near the bottom of a fully filled open tank of height \(2 m\). Taking \(g = 10 m ∕ s^2\), the rate of flow of water through the open hole would be nearly

(1). \(6.4 \times 10^{−6}\,m^3 ∕s\)
(2). \(12.6 \times 10^{−6}\,m^3 /s\)
(3). \(8.9 \times 10^{−6}\, m^3 /s\)
(4). \(2.23 \times 10^{−6}\,m^3 ∕s\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

When a block of mass M is suspended by a long wire of length L, the length of the wire becomes (L + l ). The elastic potential energy stored in the extended wire is

(1). \(\displaystyle \frac{1}{2}\) MgL
(2). \(\displaystyle Mgl\)
(3). \(\displaystyle MgL\)
(4). \(\displaystyle \frac{1}{2}\,Mgl\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A soap bubble, having radius of 1 mm, is blown from a detergent solution having a surface tension of \(2.5 × 10^{−2}N ∕ m\). The pressure inside the bubble equals at a point \(Z_0\) below the free surface of water in a container. Taking \(g = 10 m ∕ s^2\), density of water = \(10^3kg ∕ m^3\), the value of \(Z_0\) is

(1). 0.5 cm
(2). 100 cm
(3). 10 cm
(4). 1 cm

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A small sphere of radius \('r'\) falls from rest in a viscous liquid. As a result, heat is produced due to viscous force. The rate of production of heat when the sphere attains its terminal velocity, is proportional to

(1). \(r^3\)
(2). \(r^2\)
(3). \(r^5\)
(4). \(r^4\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

Two wires are made of the same material and have the same volume.The first wire has cross-sectional area A and the second wire has cross-sectional area 3A. If the length of the first wire is increased by \(\Delta l \) on applying a force \(F\) , how much force is needed to stretch the second wire by the same amount?

(1). \(9 F \)
(2). \(6 F \)
(3). \(4 F\)
(4). \(F\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

The power radiated by a black body is \(P\) and it radiates maximum energy at wavelength, \(\lambda_0\). If the temperature of the black body is now changed so that it radiates maximum energy at wavelength \(\displaystyle \frac{3}{4} \lambda_0\), the power radiated by it becomes \(n\,p\). The value of n is

(1). \(\displaystyle \frac{3}{4}\)
(2). \(\displaystyle \frac{4}{3}\)
(3). \(\displaystyle \frac{256}{81}\)
(4). \(\displaystyle \frac{81}{256}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

Two rods \(A\) and \(B\) of different materials are welded together as shown infigure. Their thermal conductivities are \(K_1\) and \(K_2\) The thermal conductivity of the composite rod will be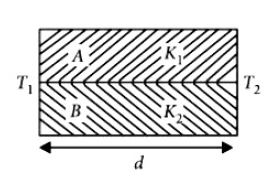


(1). \(\displaystyle \frac{3\left(K_1 + K_2\right)}{2}\)
(2). \(K_1 + K_2\)
(3). \(2\left(K_1 + K_2\right)\)
(4). \(\displaystyle \frac{K_1 + K_2}{2}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A spherical black body with a radius of \(12\, \text{cm}\) radiates \(450\, \text{watt}\) power at \(500\, \text{K}\). If the radius were halved and the temperature doubled, the power radiated in watt would be

(1). \(450\)
(2). \(1000\)
(3). \(1800\)
(4). \(225\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

The bulk modulus of a spherical object is \('B'\). If it is subjected to uniform pressure \('p'\) the fractional decrease in radius is

(1). \(\displaystyle \frac{B}{3p}\)
(2). \(\displaystyle \frac{3p}{B}\)
(3). \(\displaystyle \frac{p}{3B}\)
(4). \(\displaystyle \frac{P}{B}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

Coefficient of linear expansion of brass and steel rods are \(\alpha_1\) and \(\alpha_2\). Length of brass and steel rods are \(l_1\) and \(l_2\) respectively. If \(\left(l_2 − l_1\right)\) is maintained same at all temperatures, which one of the following relations holds good?

(1). \({\alpha_1}^2 l_2 = {\alpha_2}^2l_1\)
(2). \(\alpha_1 l_1 = \alpha_2 l_ 2\)
(3). \(\alpha_1 l_ 2 = \alpha_2 l_1\)
(4). \(\alpha_1 l_ 2^2 = \alpha_2 l_1^2\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A piece of ice falls from a height h so that it melts completely. Only one-quarter of the heat produced is absorbed by the ice and all energy of ice gets converted into heat during its fall. The value of \(h\) is [Latent heat of ice is \(3.4 × 10^5 J/kg\) and \(g = 10 N/kg\)

(1). \(136\, \text{Km}\)
(2). \(68\, \text{Km}\)
(3). \(34\, \text{Km}\)
(4). \(544\, \text{Km}\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

A black body is at a temperature of \(5760\, \text{K}\). The energy of radiation emitted by the body at wavelength \(250\, \text{nm}\) is \(\text{U}_1\),at wavelength \(500\, \text{nm}\) is \(\text{U}_2\) and that at \(1000\, \text{nm}\) is \(\text{U}_3\) Wien's constant, \(\text{b}\, =\, 2.88 \times 10^6\, \text{nmK}\). Which of the following is correct?

(1). \(\text{U}_1\, >\, \text{U}_2\)
(2). \(\text{U}_2\, >\, \text{U}_1 \)
(3). \(\text{U}_1 \,=\, 0\)
(4). \(\text{U}_3\, =\, 0\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02

Two non-mixing liquids of densities \(p\) and \(np \left(n > 1\right)\) are put in a container. The height of each liquid is \(\text{"A"}\). A solid cylinder of length \(\text{L}\) and density \(\text{d}\) is put in this container. The cylinder floats with its axis vertical and length \(pL \left(p < 1\right)\) in the denser liquid. The density \(d\) is equal to

(1). \(\{2 + \left(n − 1\right)p\}\rho\)
(2). \(\{1 + \left(n − 1\right)p\}\rho\)
(3). \(\{1 + \left(n + 1\right)p\}\rho\)
(4). \(\{2 + \left(n + 1\right)p\}\rho\)

Number of Attempts: 2

Correct Attempts: 1

Time Taken: 00:04

Average Time: 00:02