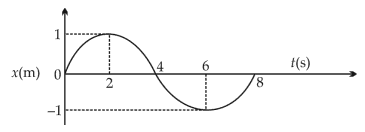
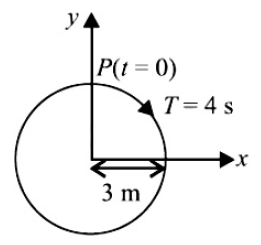
Home >> Topics >> Oscillations
Questions Not AttemptedQuestions Attempted
Unattempted Questions
Questions Available: 15
Year: 2019
Topic: Oscillations
1.
The displacement of a particle executing simple harmonic motion is given by \(y = A_0 + A sin ω t + B cos ω t\). Then the amplitude of its oscillation is given by
(1).
\(A + B\)
(2).
\( A_0 + \sqrt{A^2 + B^2}\)
(3).
\(\sqrt{A^2 + B^2}\)
(4).
\(\sqrt{{A_0}^2 + \left(A + B\right)^2}\)

Test
Solution
Year: 2025
Topic: Oscillations
2.
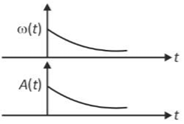
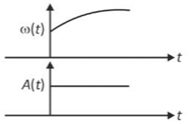
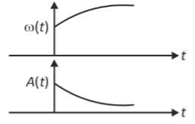
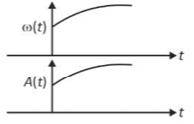
In an oscillating spring mass system, a spring is connected to a box filled with sand. As the box oscillates, sand leaks slowly out of the box vertically so that the average frequency \(\omega\left(\text{t}\right)\) and average amplitude \(\text{A}\left(\text{t}\right)\) of the system change with time t. Which one of the following options schematically depicts these changes correctly?
(1).
(2).
(3).
(4).

Test
Solution
Year: 2025
Topic: Oscillations
3.
Two identical point masses P and Q, suspended from two separate massless springs of spring constants \(\text{k}_1\) and \(\text{k}_2\), respectively, oscillate vertically. if their maximum speeds are the same, the ratio (\( \text{A}_Q\)/\(\text{A}_P\)) of the amplitude \(\text{A}_Q\) of mass Q to the amplitude \(\text{A}_P\) of mass P is
(1).
\(\displaystyle \sqrt{\frac{\text{K}_1}{\text{K}_2}}\)
(2).
\(\displaystyle \frac{\text{K}_2}{\text{K}_1}\)
(3).
\(\displaystyle \frac{\text{K}_1}{\text{K}_2}\)
(4).
\(\displaystyle \sqrt{\frac{\text{K}_2}{\text{K}_1}}\)

Test
Solution
Year: 2024
Topic: Oscillations
4.
If \(x = 5sin (πt + π/3) m\) represents the motion of a particle executing simple harmonic motion, the amplitude and time period of motion,respectively, are
(1).
\(5cm,\, 2s\)
(2).
\(5m, \, 2s\)
(3).
\(5cm, \, 1s\)
(4).
\(5m,\, 1s\)

Test
Solution
Year: 2024
Topic: Oscillations
5.
If the mass of the bob in a simple pendulum is increased to thrice its original mass and its length is made half its original length, then the new time period of oscillation is \(x/2\) times its original time period. Then the value of x is:
(1).
\(\sqrt{3}\)
(2).
\(\sqrt{2}\)
(3).
\(2 \sqrt{3}\)
(4).
\(4\)

Test
Solution
Year: 2023
Topic: Oscillations
6.
The x-t graph of a particle performing simple harmonic motion is shown in the figure. The acceleration of the particle at \(t = 2s\) is
(1).
\(\displaystyle \frac{-π^2}{8} ms^{-2}\)
(2).
\(\displaystyle \frac{π^2}{16}ms^{-2}\)
(3).
\(\displaystyle \frac{-π^2}{16} ms^{-2}\)
(4).
\(\displaystyle \frac{π^2}{8} ms^{-2}\)

Test
Solution
Year: 2022
Topic: Oscillations
7.
Two pendulums of length \(121\, cm\) and \(100\, cm\) start vibrating in phase. At some instant, the two are at their mean position in the same phase. The minimum number of vibrations of the shorter pendulum after which the two are again in phase at the mean position is:
(1).
\(11\)
(2).
\(9\)
(3).
\(10\)
(4).
\(8\)

Test
Solution
Year: 2021
Topic: Oscillations
8.
A body is executing simple harmonic motion with frequency\(\, 'n'\), the frequency of its potential energy is
(1).
\(n\)
(2).
\(2n\)
(3).
\(3n\)
(4).
\(4n\)

Test
Solution
Year: 2021
Topic: Oscillations
9.
A spring is stretched by 5 cm by a force 10 N. The time period of the oscillations when a mass of 2 Kg is suspended by it is
(1).
0.628 S
(2).
0.0628 S
(3).
6.28 S
(4).
3.14 S

Test
Solution
Year: 2020
Topic: Oscillations
10.
The phase difference between displacement and acceleration of a particle in a simple harmonic motion is:
(1).
\(\displaystyle \frac{3\,\pi}{2}\) rad
(2).
\(\displaystyle \frac{\pi}{2}\) rad
(3).
\(zero\)
(4).
\(\pi \) rad

Test
Solution
Year: 2019
Topic: Oscillations
11.
Average velocity of a particle executing SHM in one complete vibration is
(1).
\(\displaystyle \text{zero}\)
(2).
\(\displaystyle \frac{Aω}{2}\)
(3).
\(\displaystyle Aω\)
(4).
\(\displaystyle \frac{Aω^2}{2}\)

Test
Solution
Year: 2019
Topic: Oscillations
12.
The radius of circle, the period of revolution, initial position and sense of revolution are indicated in the figure.

y - projection of the radius vector of rotating particle \(P\) is
(1).
\(y(t) = 3 cos \left(\frac{πt}{2}\right)\), where y in m
(2).
\(y(t) = −3 cos 2 π t\), where y in m
(3).
\(y(t) = 4 sin \left(\frac{πt}{2}\right)\), where y in m
(4).
\(y(t) = 3 cos \left(\frac{3πt}{2}\right) \), where y in m

Test
Solution
Year: 2018
Topic: Oscillations
13.
A pendulum is hung from the roof of a sufficiently high building and is moving freely to and fro like a simple harmonic oscillator. The acceleration of the bob of the pendulum is \(20ms^{−2}\) at a distance of 5m from the mean position. The time period of oscillation is
(1).
\(2πs\)
(2).
\(πs\)
(3).
\(2s\)
(4).
\(1s\)

Test
Solution
Year: 2017
Topic: Oscillations
14.
A spring of force constant k is cut into lengths of ratio \(1 : 2 : 3\). They are connected in series and the new force constant is \(k'\).Then they are connected in parallel and force constant is \(k''\).Then \(k' : k''\) is
(1).
\(1 : 9\)
(2).
\(1 : 11\)
(3).
\(1 : 14\)
(4).
\(1 : 6\)

Test
Solution
Year: 2017
Topic: Oscillations
15.
A particle executes linear simple harmonic motion with an amplitude of \(3\, \text{cm}\). When the particle is at \(2\, \text{cm}\) from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is
(1).
\(\displaystyle \frac{\sqrt{5}}{2π}\)
(2).
\(\displaystyle \frac{4π}{\sqrt{5}}\)
(3).
\(\displaystyle \frac{2π}{\sqrt{3}}\)
(4).
\(\displaystyle \frac{\sqrt{5}}{π}\)

Test
Solution